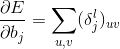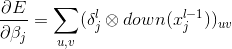Machine Learning 基础公式
Machine Learning 基础公式
Model and Representation
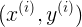表示第i个样本
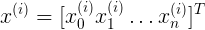表示第i个样本中，x的n个特征
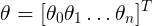表示模型的参数
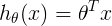表示hypothesis对样本的预测结果
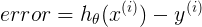表示对第i个样本的预测值与实际结果的误差，h与y都为一数值，二分类 非0即1
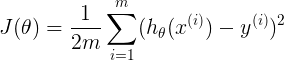表示预测结果与实际结果的cost，为数值
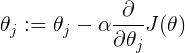表示对第j个参数求导，直到收敛；用上一周期的参数，一次性更行所有参数，非用最新值更新本次参数
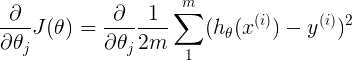表示对cost function的theta计算
Logical Regression
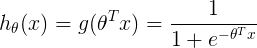表示对logistic regression的hypothesis公式，输出一个数值（0或1）
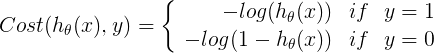表示对不同的y时，cost的表示
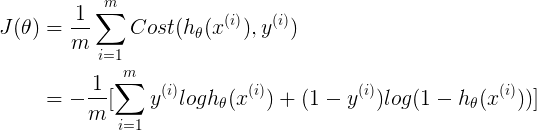表示统一的logistic regression cost function，y{i}为{0,1}，y{i}<1x1>，thetaT<1xn>，x{i}
Multiclass classification
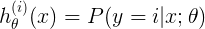表示对特定的x与theta，对样本分类，预测样本属于i类的概率
Regularization
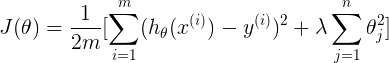表示对theta1-thetan进行限制，不包括theta0
Regularized linear regression
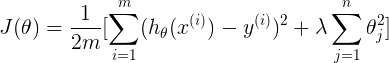表示线性回归的正则化的使用
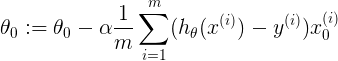表示求梯度时，对theta0求导，由于其不使用正则化，因此保持不变
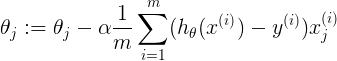表示线性回归求导，其中x{j}(i)表示第i个样本中，第j维特征，不包含正则化
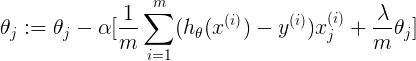表示用正则化后的J，求导
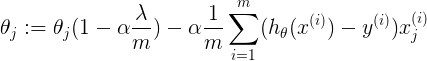表示首项中，thetaj参数<1，则thetaj变小，其影响值也小，而第二项与上式一致，则降低了thetaj，使某些thetaj不起作用
Regularized logistic regression
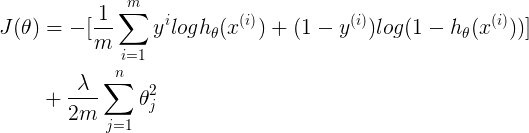表示逻辑回归中，正则化对Cost的约束
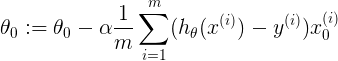表示求梯度时，对theta0求导，由于其不使用正则化，因此保持不变
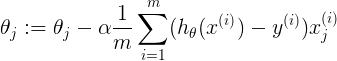表示逻辑 回归求导，其中x{j}(i)表示第i个样本中，第j维特征，不包含正则化
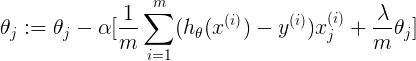表示用正则化后的J，求导。上述三个相似，但是由于
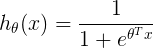，这为主要不同之处
Neural Network
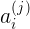表示第j层，第 i 个神经元的输入激励
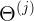表示weights矩阵，从 j 到 j+1 层的隐射关系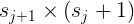 
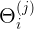表示从 j 层所有神经元到 j+1 层的第 i 个神经元，对应的参数；即 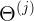中第i行为 j 层到 j+1 层的第 i 个神经元，需要的 s{j}+1 个参数，j+1层总共有 s{j+1}个神经元
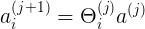表示 j+1 层与 j 层之间的连接关系
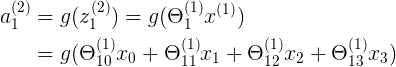
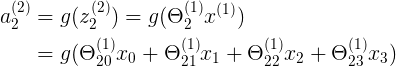
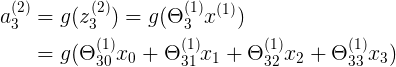
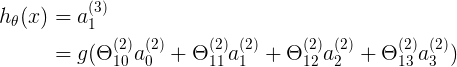
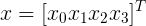<4x1>
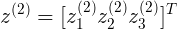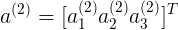<3x1>
<3x1>
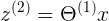<3x4> x <4x1> = <3x1>
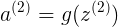<3x1> = <3x1>
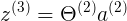<1x4> x <1+3x1> 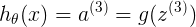= <1x1>
<1x1>
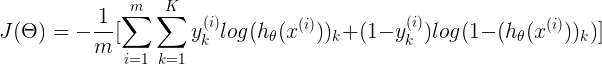其中h(x)
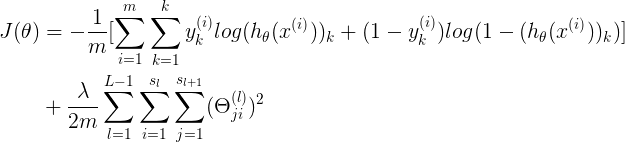表示neural network中，加了正则项的cost function
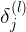表示第 l 层上第 j 个节点的误差error
NN example
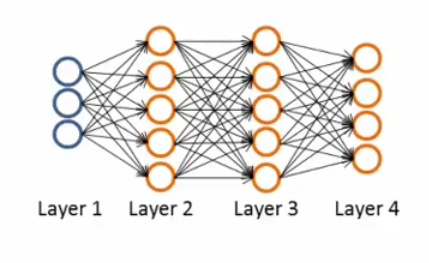表示四层neural network
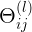表示正向pass中，在 l 层上，第 j 个神经元对应，l+1层上，第 i 个神经元的权值系数
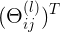表示反向pass中，在 l+1 层上，第 i 个神经元对应，l 层上第 j 个神经元
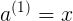<4X1>
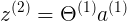Theta1<5x4> a1<4x1> = z2<5x1>
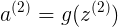a2<6x1> 增加a2{0}
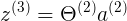Theta2<5x6> a2<6x1> = z3<5x1>
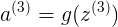a3<6x1> 增加a3{0}
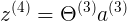Theta3<4x6> a3<6x1> = z4<4x1>
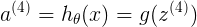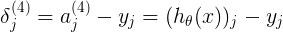
a4<6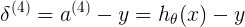x1>
<4x1>
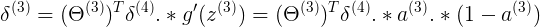<6x1> Theta3{T}<6x4> delta4<4x1> a3<6x1> (1-a3) <6x1> （根据连接关系，反向推导delta3，参考Week5 Cost Function and Backpropagation）
（上述公式与下面矩阵就J(Theta)公式相似，只不过增加了对激励函数求导的计算）
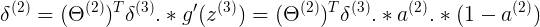<6x1> Theta2{T}<6x5> delta3<5x1> （由于delta3计算了bias，但是bias只被计算，不参加反向。因此delta3由<6x1>变为<5x1>） a3<6x1> (1-a3) <6x1>
第一层为输入层，只是观察使用，不使用误差计算
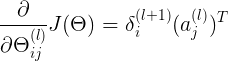<s{j+1} x s{j}+1> delta{l+1}<(s{j+1}) x 1> a{l}<1 x s{j}+1>
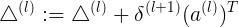<s{l+1} x s{l}+1> 这里一个Delata代表一个样本，相加表示对所有m个样本计算总梯度
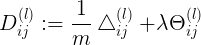<s{l+1} x s{l}+1> 这里Delta除以m，表示求m个样本的平均梯度，lambda表示正则项的约束
（对于单个样本，且不计算正则化的情况下，网络梯度为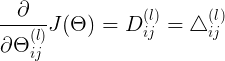
）
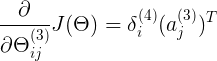<4x6> delta4<4x1> a3T<1x6> （可用矩阵行列乘法，理解其计算意义）
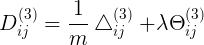<4x6> 3到4层连接的样本平均梯度（可忽略正则项）
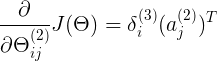<5x6> delta3<5x1>(bias不参与反向传播，减1个) a2T<1x6>
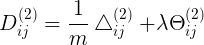<5x6> 2到3层连接的样本平均梯度
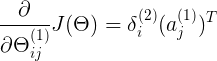<5x4> delta2<5x1>(bias不参与反向传播，减1个) a1T<1x4>
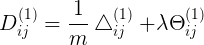<5x4> 1到2层连接的样本平均梯度
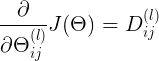最终i梯度计算结果的表示
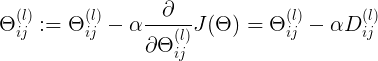更新连接weights计算
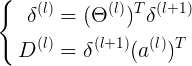先计算delta，计算误差<s{l} x 1>；再计算D梯度，使用之前计算的delta<s{l+1} x s{l}+1>
CNN example
表示第 l 层上第 j 个feature map
卷积层前向：
表示经过convolution，第 l 层上第 j 个feature map由 l-1 层计算得到，其中k{l}表示 l-1 层到 l 层的连接卷积权值，与之前的表示形式不一样
Subsampling层后向：
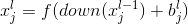表示经过subsampling，第 l 层上第 j 个feature map由 l-1 层计算得到，这里feature map的个数不变，都是 j 个，down()表示对像素点进行相加求和
卷积层后向误差：
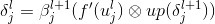表示经过 l+1 层的delta{l+1}反向传播到 l 层得到delta{l}，其中up表示将 1x1 像素拓展为 NxN 像素
subsampling层后向误差：
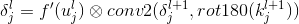表示经过 l+1 层的delta{l+1}反向传播到 l 层得到delta{l}
卷积层梯度求导：
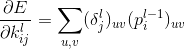
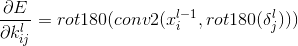
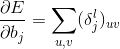
subsampling梯度求导：
