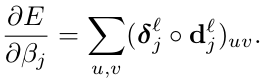本文章主要参考了三遍博客：zouxy09的CNN卷积神经网络推导和实现 ，tornadomeet的CNN的反向求导及练习和仙守的Notes on Convolutional Neural Networks。

介绍

本文主要讨论了CNN的推导和实现，并加上一些简单的扩展。

用BP训练全连接网络

在介绍卷积网络算法之前，先介绍标准的BP算法。

前向过程

在推导过程中，损失函数为误差平方和损失函数。对于c类和N个训练样本的多分类问题，误差定义为：

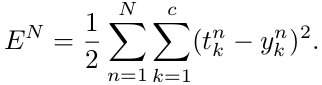
其中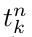，是第n个样本对应的label的第k个维度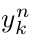，是第n个输入样本对应的输出层第k个单元的输出值。如果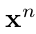属于第k类，则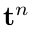的第k维为正，其余维的值为负或零，具体数值是根据激励函数决定的。

因为整个训练集的误差是每个样本的误差的总和，所以在这里可以只考虑一个样本进行BP

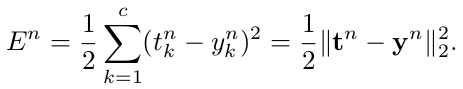
对于通常的全接连层，可以使用反向规则计算E对于网络权值的导数。让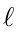表示当前层，定义当前层的输出为：

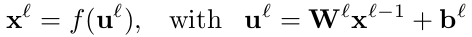
反向过程

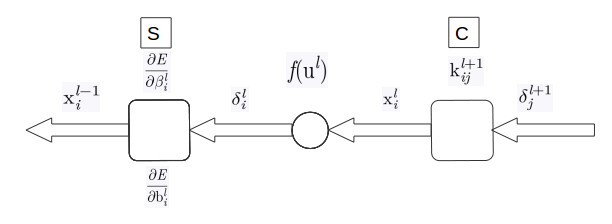
网络中，后向传播的误差可以被人为是每个单元关于偏置项扰动的敏感性：

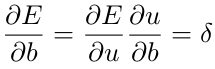
从高层到底层的反向求导，可以使用下列关系式：

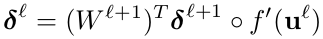
其中，o表示点乘。而输出层的敏感度有一些不同：

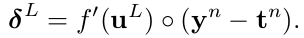
最后，对于某个给定的神经元的权值更新的规则就是对该神经元的输入部分进行复制，用神经元的delta进行缩放。用向量形式，相当于计算输入向量（前一层的输入）和该神经元delta向量的外积。

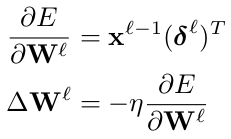
卷积神经网络

卷积层

这里讨论卷积层的反向求导更新。每个输出map将多个输入map与卷积相结合

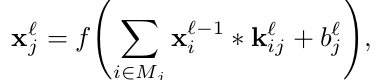
这里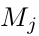，表示输入maps的选择，Matlab的卷积形式为’valid’。每个输出map都有一个额外的bias，然而对于一个具体的输入map而言，输出图是有着不同的卷积kernel。比如，输出map j和map k都是由输入map i求和得到的，然而应用在输入map i上求输出map j和map k的卷积kernel是不同的。

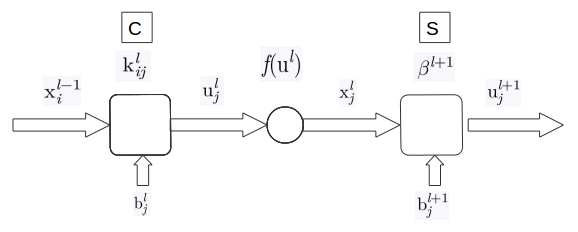
其中，k{ij}为反向的，即经过翻转的，其余项皆为正向

计算卷积层梯度

假设convolution层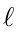后都跟着一个sub-sampling层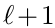。在反向传播算法中，为了计算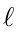层的单元的敏感度，应该先计算与当前层该单元相关联的下一层的敏感度总和，再乘以下一层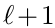层与这个单元之间的权重参数，来得到传递到当前层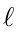的敏感度，并用当前层的输入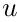的激活函数的导数乘以上述结果。在一个convoluton层后紧跟着sub-sampling层的情况下，在下一层（sub-sampling层）中的一个像素，其相关联的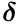都对应着convolution层输出map的一块像素。因此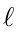层中map上的每个单元都只与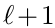上对应map的一个单元相连接。为了使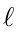的敏感度计算更高效，在sub-sampling层的敏感度map上使用upsample操作，使其与convolution层的map相同尺寸，随后将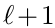层的upsample敏感图与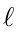层的激活函数导数map点乘。在sub-sampling层的权值定义为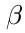。在convolution层的每个map j中进行同样计算，用sub-sampling层的map进行匹配。

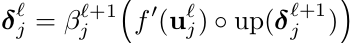
这里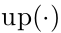，表示upsample操作，如果upsample操作因子为n，则输入像素进行水平和竖直的复制n次操作。使用Kronercker高效实现：

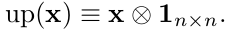
现在有了对于给定map的敏感度，通过对delta的简单求和计算bias梯度：

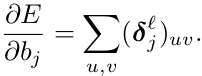
最终，计算kernel权值的梯度，通过将所有连接中与该权值有关的权值梯度相加，与bias操作类似：

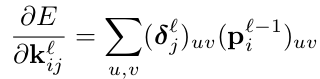
其中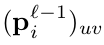，表示输入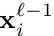的patch，在卷积操作时用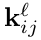进行点乘，来计算卷积的输出map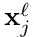的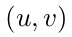位置元素。这里可通过Matlab函数实现计算：

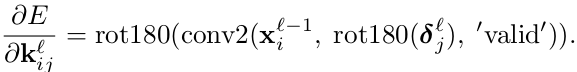
这里，翻转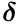是为了进行相关操作而不是卷积，再将输出翻转回来，使在进行前向过程中，kernel保持预定方向。（在网络中，kernel的方向是翻转的，即反向；其余的皆为正向；conv2函数在卷积过程中，会将第二个参数矩阵翻转为反向，因此在输入时，先将delta翻转，则计算过程中会自动转为正向；通过conv2函数得到的kernel是正向的，由于kernel在网络中的方向原来就是方向的的，那么其所导数也需要是反向的，则需要经过rot180处理，翻转为反向）

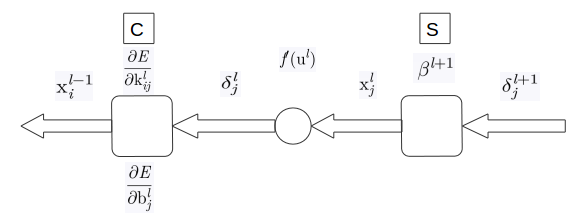
其中，{E/k}为反向的，即经过翻转的，其余项为正向的。这里的delta和相同位置的u的size维度相同。

Sub-sampling层

sub-sampling层生成输入maps的下采样版本。如果N个输入map，则有N个输入map，但是输入map的size会更小

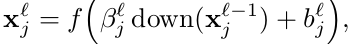
这里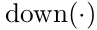，表示下采样函数。每个输出map都有对应的乘法偏置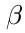和额外bias。

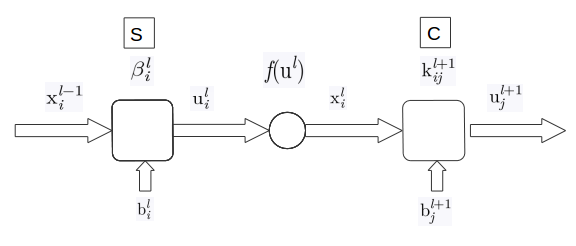
其中kernel为反向，其余项都为正向，这里的 i 相当于公式中的 j

计算梯度

计算梯度的困难在于计算敏感度map。一旦得到敏感度map，所要更新的学习参数只有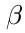和bias。假设sub-sampling层前后都是convolution层。如果sub-sampling后是全连接层，则sub-sampling层的敏感度map可由上述全连接层的反向公式计算。

当我们尝试计算kernel梯度时，必须知道输入map中哪个patch对应输出map的像素。这里，我们必须知道当前层的敏感度map的patch对应于下一层敏感度map的像素，为了使用delta计算公式。在输入patch和输出像素的连接上相乘的权值是翻转过的卷积kernel的权值。（即相对于正向的kernel而言，这里计算的权值应该是经过翻转的）。通过下式也可实现快速计算：

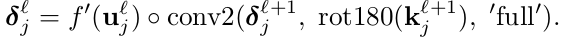
类似之前的操作，翻转kernel使卷积函数进行相关操作。（网络中的kernel都为反向，rot180(k)使原本反向的kernel为正向，而conv2函数中会再次将kernel翻转，满足之前反向卷积计算公式中的要求：即kernel是翻转状态的条件）。’full’参数下，当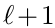层的一个神经元的输入数量不是完整的nxn大小的卷积kernel时，可以快速高效地处理边缘。这种情况下，’full’会在丢失的部分自动补零。

计算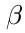和bias的梯度，额外的bias同样是对敏感度map的元素相加得到的：

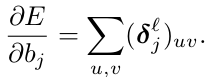
乘数偏置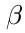包含了前向过程中在当前层计算得到的原始下采样map。因此，在前向计算中，保存map是非常有用的，就不用在反向计算时重新计算了。

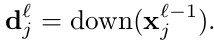
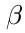的梯度由下式计算：