论文解读《Notes on Convolutional Neural Networks》
Paper Reading
Introduction
本文讨论了CNN的推导与实现,以及一些简单的拓展内容。CNN包含了很多比权值更多的连接个数;在框架上(architecture),它实现了正则化的一种形式。另外,CNN提供了一定程度的平移不变性(translation invariance)。这种特殊形式的神经网络,假设了我们需要学习用数据驱动的filter,作为一种提取描述输入的特征的方法。在此文的推导中,是用二维数据与卷积进行的,但是可以不需多余的代价,即可转化为任意维数的实现
在此,先进行全连接层的典型反向传播介绍,接着是在2D卷积层中,反向传播对filiter以及下采样(subsampling)层的更新。通过讨论,我们突出强调了实现的有效性,以及一小段Matlab代码来对应等式。随后,再讨论如何结合从之前的各层中的特征映射(feature maps)。
Vanillar Back-propagation Through Fully Connected Networks
在典型的卷积神经网络中,早期的分析主要是改变convolution和sub-sampling操作,然而,框架(architecture)中最后部分是,多个1维的全连接层。但你想要将最后的2D feature map作为1D全连接层的输入,一个简便的做法便是将在输出map上的feature,转换为一个长的输入向量。分析CNN的算法前,先讨论标准的反向传播算法。
Feedforward Pass
推到公式中,使用平方误差损失函数(squared-error loss function)
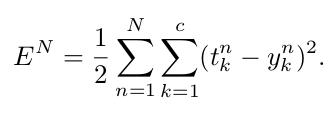
t_k_n中,第n个模式对应的第k维特征;y_k_n是第n个输入模式对应的输出层的第k个值。对于多类分类问题,如果X_n对应第k类,则t_n的第k个值是正的。根据你activation function,t_n的其他值可能是零或者负值。
因为整个数据集的错误率只是每个样本错误率之和,
Backpropagation Pass
Convolutional Neural Networks
传统的卷积层注重sub-sampling层,来减少计算实际,以及简历更深的空间与结构不变性。小的sub-sampling因素是需要的,同时为了保持specificity(特异性)。这个想法并不是新的,但是概念却是简单实用的。动物的视觉突触与听觉神经已经被研究了过去几十年。多层次的分析与学习框架可能成为听觉领域成功的关键。


